கதிர் ஒளியியல்

அலகு 6

ஒளியியல் (OPTICS)

ஒரு காலம் இருண்டதாக இருப்பதற்கு ஒளி வீச மறுப்பது காரணமல்ல, மக்கள் காண மறுப்பதே காரணமாகும்.

                                                                  - ஜேம்ஸ் ஆல்பர்ட் மிச்சனர்

கற்றலின் நோக்கங்கள்

இந்த அலகில் மாணவர்கள் அறிந்து கொள்ள இருப்பது

• ஒளியைக் கதிராகவும், அலையாகவும் கருதும் இரு கருத்துக்கள்

• ஒளிபரவுதலும் மற்றும் அதன் பண்புகளும்

• சமதள ஆடி, லென்ஸ் மற்றும் முப்பட்டகத்தோடு தொடர்புடைய கருத்துகள்

• நுண்ணோக்கி, தொலைநோக்கி போன்ற ஒளியியல் கருவிகளின் செயல்பாடுகள்

• உருப்பெருக்கம், பிரிதிறன் போன்ற பல்வேறு வரையறைகள்

• ஒளியின் அலைப்பண்பை நிரூபிக்கத் துணைபுரியும் பல்வேறு நிகழ்வுகள்

அறிமுகம்

ஒளி புதிரான ஒன்றாகும். ஆனாலும் அதன் பண்புகள், நம்மைப் பரவசத்தில் ஆழ்த்துகின்றன. ஒளியை ஒரு தனித்துவமாக நம்மால் முழுவதும் புரிந்துகொள்ள இயலாது. இந்த அலகில் நாம் கதிர் ஒளியியல் மற்றும் அலை ஒளியியல் என்ற இருவேறு கொள்கைகளை படிக்க உள்ளோம். கதிர் ஒளியியல், ஒளியை நேர்க்கோட்டில் செல்லும் ஒரு கதிராகப் பார்க்கிறது. இக்கதிரினைக் கொண்டு வரையப்பட்ட கதிர்ப்படங்கள் ஒளிக்கதிரின் பல்வேறு பண்புகளைப் புரிந்து கொள்ள நமக்குத் துணைபுரிகின்றன. அலை ஒளியியல், ஒளி அலையாகப் பரவும் போது ஏற்படும் நிகழ்ச்சிகளைப்பற்றி நமக்கு விளக்குகின்றது. முதலில் கதிர் ஒளியியலைப் பற்றி அறிந்துகொண்டு பின்னர், அலை ஒளியியலைப் பற்றி நாம் படிக்கலாம்.

கதிர் ஒளியியல்

கதிர் ஒளியியலில், ஒளி ஒரு கதிராகக் கருதப்படுகிறது. இக்கதிர், ஊடகம் ஒன்றினுள் நேர்க்கோட்டில் செல்கிறது. அவ்வொளி, மற்றொரு ஊடகத்தினுள் நுழையும் போது அல்லது தடையின் மீது மோதும் போது, தனது நேர்க்கோட்டுப் பாதையிலிருந்து விலகல் அடையும்.

ஒளிக்கதிர் என்பது ஒளி செல்லும் திசையைப் பற்றிய தகவலை மட்டுமே நமக்கு தரும். ஒளியின் மற்ற பண்புகளான ஒளிச்செறிவு, நிறங்கள் போன்றவற்றைப் பற்றிய தகவல்களைக் கதிர் ஒளியியலிலிருந்து நாம் பெற இயலாது. இருந்தபோதிலும் ஒளியைப்பற்றி புரிந்துகொள்ள ஒளியைக் கதிராகக் கருதும் இம்முறை ஓர் அறிவார்ந்த செயலாகும். ஒளி ஒன்றின் பாதையை ஒளிக் கதிர் என்றும், இக்கதிர்களின் தொகுப்பினை ஒளிக்கற்றை என்றும் அழைக்கலாம். இந்த அலகில் கதிர் ஒளியியலின் அடிப்படையில் ஒளி எதிரொளிப்பு, ஒளிவிலகல் மற்றும் ஒளிச்சிதறல் போன்ற நிகழ்வுகளைப்பற்றி நாம் அறிந்து கொள்வோம்.

எதிரொளிப்பு

ஊடகத்தினுள் செல்லும் ஒளிக்கதிர் எதிரொளிக்கும் பரப்பில் பட்டு, அதே ஊடகத்தினுள் பின்னோக்கி வரும் நிகழ்ச்சிக்கு எதிரொளிப்பு என்று பெயர். பளபளப்பான பரப்புகள் ஒளியை நன்கு எதிரொளிக்கும். பின்புறம் வெள்ளிப்பூச்சு (silver coated) செய்யப்பட்ட கண்ணாடி, அதன்மீது விழும் 90% ஒளியை எதிரொளிக்கும் தன்மை கொண்டவை. படுகோணம் (i) மற்றும் எதிரொளிப்புக் கோணம் (r) இவற்றை ஒளி எதிரொளிக்கும் புள்ளியில், எதிரொளிக்கும் பரப்புக்குச் செங்குத்தாக வரையப்பட்ட செங்குத்துக் கோட்டைப் பொருத்து அளவிடலாம். ஒளி எதிரொளிப்பு விதியின்படி,

(அ) படுகதிர், எதிரொளிப்புக் கதிர் மற்றும் எதிரொளிக்கும் பரப்புக்கு செங்குத்துக்கோடு இவை அனைத்தும் ஒரே தளத்தில் அமையும்

(அதாவது ஒரே பரப்பில் காணப்படும்).

(ஆ) படுகோணம் (i) மற்றும் எதிரொளிப்புக் கோணம் (r) இவை இரண்டும் ஒன்றுக்கொன்று சமம்.

i = r            (6.1)

ஒளி எதிரொளிப்பு விதி படம் 6.1 இல் காட்டப்பட்டுள்ளது

எதிரொளிக்கும் பரப்பு, சமதளமாகவோ அல்லது வளைபரப்பாகவோ எவ்வாறு இருப்பினும் பரப்பின் ஒவ்வொரு புள்ளியிலும் ஒளி எதிரொளிப்பு விதி பொருந்தும். எதிரொளிக்கும் பரப்பு சமதளமாக இருப்பின் ஒளி எதிரொளிப்பு விதியின்படி, இணையாகக் செல்லும் படுகதிர்கள், எதிரொளிப்புக்குப்பின்பும்

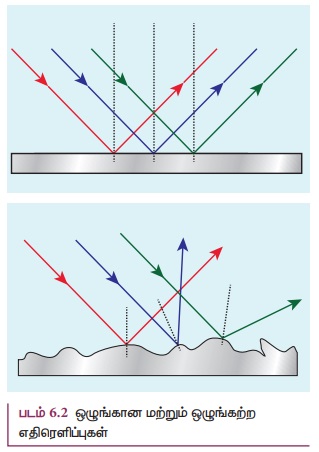
இணையாகவே வரும். எதிரொளிக்கும் பரப்பு ஒழுங்கற்று இருந்தால் இணையாகச் செல்லும் படுகதிர்கள், எதிரொளிப்புக்குப் பின்னர் ஒழுங்கற்று வரும். இது படம் 6.2 இல் காட்டப்பட்டுள்ளது

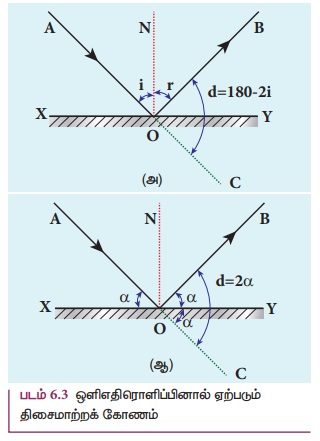
ஒளி எதிரொளிப்பினால் ஏற்படும் விலகுகோணம்

படுகதிர் மற்றும் விலகுகதிர் இவற்றுக்கு இடையே உள்ள கோணத்திற்கு விலகுகோணம் என்று பெயர். இவ்விலகுகோணத்தைப் படம் 6.3(அ) இல் காட்டியுள்ளவாறு எளிய வடிவியல் மூலம் கணக்கிடலாம். படுகதிரை AO எனவும் எதிரொளிப்புக்கதிரை OB எனவும் கொள்க. படுகதிரின் தொடர்ச்சியாகக் கருதப்படும் OCஐ விலகுகதிர் எனக்கருதுக. OBமற்றும் OCஇவற்றுக்கு இடையே உள்ள கோணமே விலகுகோணம் (d) ஆகும். வடிவியல் கணக்கீட்டின்படி,d= 180 - (i+r) ஒளி எதிரொளிப்பு விதியின்படி i = r. எனவே, ஒளி எதிரொளிப்பினால் ஏற்படும் விலகுகோணத்தைப் பின்வருமாறு எழுதலாம்.

d = 180 – 2i       (6.2)

ஒளி எதிரொளிப்பினால் ஏற்படும் விலகுகோணத்தை, நோக்கு கோணத்தின் (a) அடிப்படையிலும் கணக்கிடலாம். படம் 6.3(ஆ) இல் காட்டியுள்ளவாறு படுகதிர் AO மற்றும் எதிரொளிக்கும் சமதளப்பரப்பு XY இவற்றுக்கு இடையே உள்ள கோணம் நோக்கு கோணம் (a) ஆகும். வடிவியல் கணக்கீட்டின்படி கோணங்கள் ∠AOX = a, ∠BOY = a மற்றும் ∠YOC = a (இவை அனைத்தும் ஒன்றே). படத்திலிருந்து விலகுகோணம் (d) என்பது கோணம் ∠BOC ஆகும். எனவே,

d = 2a     (6.3)

எடுத்துக்காட்டு 6.1

ஒளி எதிரொளிக்கும் பரப்பினை θ கோணம் சாய்க்கும் போது எதிரொளிக்கும் கதிர் 2θ கோணம் சாயும் என்பதை நிரூபி.

தீர்வு :

எதிரொளிக்கும் பரப்பு ABக்கு, படுகதிர் IO மற்றும் எதிரொளிப்புக்கதிர் OR₁ ஆகும். இங்கு எதிரொளிக்கும் பரப்புக்குச் செங்குத்தைப் பொருத்து (குத்துக்கோடு N) i என்பது படுகோணமாகும். இது எதிரொளிப்புக் கோணத்திற்குச் சமமாகும். இது படத்தில் காட்டப்பட்டுள்ளது. எதிரொளிக்கும் பரப்பு AB θ கோணம் சாயும். A’ B’ நிலைக்குக் கொண்டுவரும் போது, குத்துக்கோடும், N நிலையிலிருந்து N' நிலைக்கு θ கோணம் சாயும். இங்கு படுகதிர் IO மாறாமல் ஒரே நிலையில் இருப்பதை நினைவில் கொள்ள வேண்டும். சாய்க்கப்பட்ட நிலையில் படுகோணம் i+θ. எனவே, எதிரொளிப்புக்கோணமும் i+θ. ஆகும். ஆனால் சாய்க்கப்பட்ட நிலையில் எதிரொளிப்புக்கதிர் OR₂. எனவே, OR₂. மற்றும் OR₁.  க்கு இடையே ஏற்பட்டக் கோணம்

∠R_IOR₂ = ∠ZN'OR₂- ∠ZNOR_I

(i+θ) - (i-θ) = 2θ ஆகும்.

சமதள ஆடியில் பிம்பம் தோன்றுதல்

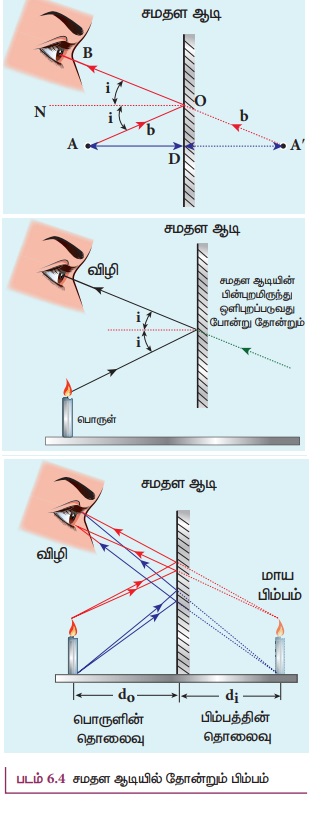
சமதள ஆடி ஒன்றின் முன்னே A என்ற புள்ளிப் பொருள் ஒன்று வைக்கப்பட்டுள்ளது எனக் கருதுக. படம் 6.4இல் காட்டியுள்ளவாறு O என்பது, படுகதிர் சமதள ஆடியில் படும் புள்ளியாகும். புள்ளிப் பொருளிலிருந்து சமதள ஆடிக்கு வரும் படுகதிர் AO, எதிரொளிப்புக் கதிர் OB, மேலும் ON என்பது, செங்குத்துக் கோடாகும்.

படுகோணம் ∠AON = எதிரொளிப்புக் கோணம் ∠BON

சமதள ஆடிக்குச் செங்குத்தாக வரும் AD என்ற மற்றொரு படுகதிர் சமதள ஆடியில் D என்ற புள்ளியில் பட்டு DA வழியே எதிரொளிக்கும். BO மற்றும் AD கதிர்களை ஆடிக்குப் பின்புறமாக நீட்டிச் செல்லும்போது அவை A' என்ற புள்ளியில் சந்திக்கின்றன. எனவே, இவ்விரண்டு கதிர்களும் ஆடிக்குப் பின்புறமுள்ள A' என்ற புள்ளியிலிருந்து வருவதுபோன்று தோன்றும். ஒரு சமதள ஆடியில் பொருள் மற்றும் அதன் பிம்பம் இரண்டும், சமதள ஆடியிலிருந்து ஒரே செங்குத்துத் தொலைவில் இருக்கும். இதனைப் பின்வருமாறு விளக்கலாம்.

படம் 6.4இல் இருந்து,

∠AON = ∠DAO [ஒன்றுவிட்ட கோணங்கள்)

∠BON = ∠OA'D (ஒத்த கோணங்கள்)

எனவே முக்கோணவியல் விதிகளின்படி

∠DAO= ∠OAD’D

மேலும், ΔODA மற்றும் ΔODA' இரண்டும் சர்வசமமான முக்கோணங்கள் ஆகும். எனவே,

:: AD = A'D

இதிலிருந்து சமதள ஆடிக்கு முன்பாகப் பொருள் எவ்வளவு தொலைவில் வைக்கப்பட்டுள்ளதோ, அதே தொலைவில் ஆடிக்கு உள்ளே பிம்பம் தோன்றும் என்பதை அறியலாம்.

சமதள ஆடியில் தோன்றும் பிம்பத்தின் பண்புகள்

(i) சமதள ஆடியில் தோன்றும் பிம்பம், இடவல மாற்றம் கொண்ட நேரான மாய பிம்பமாகும்.

(ii) பொருளின் அளவும், பிம்பத்தின் அளவும் ஒன்றுக்கொன்று சமமாகும்.

(iii) சமதள ஆடிக்கு முன்பாகப் பொருள் எவ்வளவு தொலைவில் வைக்கப்பட்டுள்ளதோ, அதே தொலைவில் ஆடிக்கு உள்ளே பிம்பம் தோன்றும்.

(iv) பொருளொன்றை θ கோணத்தில் அமைக்கப்பட்டுள்ள இரண்டு சமதள ஆடிகளுக்கு நடுவே வைக்கும்போது தோன்றும் பிம்பங்களின் எண்ணிக்கையைப் n பின்வருமாறு அறியலாம்.

*  சமச்சீரான அல்லது சமச்சீரற்ற நிலையில் பொருள் வைக்கப்பட்டிருந்தால், [360/θ]  இரட்டைப்படை எனில், n = [360 / θ -1]

* சமச்சீரான நிலையில் பொருள் வைக்கப்பட்டிருந்தால் [360 / θ] ஒற்றைப்படை எனில் n = [360 / θ -1]

* சமச்சீரற்ற நிலையில் பொருள் [360/θ] வைக்கப்பட்டிருந்தால் ஒற்றைப்படை எனில், n - [360 / θ]

சமதள ஆடியில் தோன்றும் மெய் மற்றும் மாயபிம்பங்கள்

சமதள ஆடிக்கு முன்புறம் O என்ற புள்ளியில் மெய்யான பொருள் ஒன்றை வைக்கும்போது, அப்பொருள் படம் 6.5(அ) இல் காட்டியவாறு அனைத்துத் திசைகளிலும் செல்லும் விரிகதிர்களை ஏற்படுத்தும். இவ்விரிகதிர்கள் சமதள ஆடியினால் எதிரொளிக்கப்பட்ட பின்னர், சமதள ஆடிக்குப் பின்புறம் உள்ள I என்ற புள்ளியிலிருந்து வருவதுபோன்ற தோற்றத்தை ஏற்படுத்தும். இதுபோன்று, திரையில் தோன்றாத ஆனால் கண்களினால் மட்டும் காணக்கூடிய பிம்பமே, மாயபிம்பமாகும் (virtual image)

மாறாக, குவிகதிர்கள் சமதள ஆடியில் பட்டு எதிரொளிக்கப்பட்ட பின்பு, படம் 6.5(ஆ) இல் காட்டியுள்ளவாறு 1 சமதள ஆடிக்கு முன்புறமுள்ள என்ற புள்ளி வழியே சென்று பிம்பத்தை ஏற்படுத்தும். இப்பிம்பம் ஆடிக்கு முன்புறமாக உள்ளதால் இது திரையில் தோன்றும். மேலும், இதனைக் கண்களால் காண முடியும். இவ்வகையான பிம்பத்திற்கு மெய்பிம்பம் (real image) என்று பெயர்.

பொதுவாக சமதள ஆடி மாயபிம்பத்தை மட்டுமே தோற்றுவிக்கும் என்றே நாம் கருதுகிறோம். 'ஆனால், மேற்கண்ட விளக்கத்திலிருந்து சமதள ஆடியின்மீது குவி கதிர்கள் விழும்போது, அது மெய்பிம்பத்தையும் உருவாக்கும் என்பதை நாம் புரிந்து கொள்ளவேண்டும்.

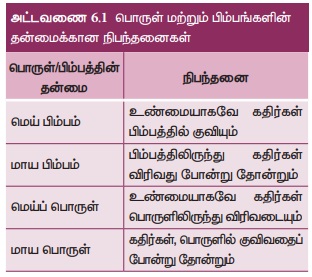
சமதள ஆடியில் தோன்றும் மெய் மற்றும் மாயபிம்பங்களைப் பற்றிய விளக்கம் அட்டவணை 6.1இல் தொகுக்கப்பட்டுள்ளது. இது கதிர் ஒளியியலில் பொருள்கள் மற்றும் பிம்பங்களின் தன்மையை அறிவதற்குப் பெரிதும் பயன்படும்.

எடுத்துக்காட்டு 6.2

ஒருவர், தம் முழு உருவத்தையும் கண்ணாடியில் பார்க்க வேண்டுமென்றால், கண்ணாடியின் உயரம் எவ்வளவு இருக்க வேண்டும்?

தீர்வு:

h உயரம் கொண்ட மனிதர் ஒருவர் செங்குத்தாக உள்ள கண்ணாடியின் முன்னே நிற்கிறார் எனக் கருதுக. அவரின் தலை மற்றும் பாதத்திலிருந்து செல்லும் ஒளிக்கதிர்கள் கண்ணாடியில் பட்டு எதிரொளித்து, அவரின் கண்களை அடைந்தவுடன், அவர், தமது தலை மற்றும் பாதங்களைக் காண்கிறார்.

அவரின் தலை (H) மற்றும் கண் (E) இரண்டிற்கும் இடைப்பட்ட தொலைவை h₁, எனவும், அவரின் பாதம் (F) மற்றும் கண் (E) இரண்டிற்கும் இடைப்பட்ட தொலைவை h₂, எனவும் கொள்க. எனவே, மனிதனின் மொத்த உயரம் h = h₁, + h₂, ஆகும்.

எதிரொளிப்பு விதியின்படி, இரண்டு கடைக்கோடி புள்ளிகளில் ஏற்படும் எதிரொளிப்புகளிலும் (extreme reflections) படுகோணமும் எதிரொளிப்புக் கோணமும் ஒன்றுக்கொன்று சமமாகும். மேலும், இவ்விரண்டு எதிரொளிப்புகளிலும் படுகதிர் மற்றும் எதிரொளிப்புக் கதிர்களுக்கு இடையே உள்ள கோணத்தின் இருசமவெட்டியே, செங்குத்துக் கோடாகும். வடிவியலின்படி மனிதரின் முழு உருவத்தையும் காண, கண்ணாடி, அவரின் உயரத்தில் பாதி அளவு இருந்தால் போதுமானதாகும். h₁, + h₂/2 = h/2

கண்ணாடியின் உயரம் , மனிதருக்கும் கண்ணாடிக்கும் இடையே உள்ள தூரத்தைச் சார்ந்ததா?